Numerical simulation of free-surface fluid flows

Lagrangian approaches to the solution of Navier-Stokes equations are very effective in modeling the fast evolution of free surfaces and interfaces, since they are automatically defined by the position of the mesh nodes, with no need for tracking algorithms.

On the other hand, as expected when using pure Lagrangian formulations with mesh-based algorithms, the mesh quickly deteriorates in time. To overcome this difficulty, when the mesh becomes too distorted, a remeshing should be performed with a highly computationally effective technique, to be repeatedly used during the analysis.

The Particle Finite Element Method (PFEM) exploits this idea making use of a Delaunay Tassellation coupled with a distortion criterion to efficiently generate a new connectivity for the mesh nodes.

The proposed approach has been applied to Newtonian and non-Newtonian fluids.

Recent contributions:

Improvements of the management of complex boundary conditions

The PFEM has been successfully employed in a number of different engineering applications, however, there are several circumstances of practical interest where the Lagrangian nature of the method makes it difficult to enforce non-homogeneous boundary conditions. A novel mixed Lagrangian–Eulerian technique is proposed to the purpose of simplifying the imposition of this type of conditions with the PFEM. The method is simple to implement and computationally convenient, since only nodes on the boundary are considered Eulerian, while nodes inside the
fluid body maintain their Lagrangian nature.

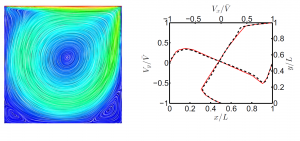
Figure: Lid-driven cavity flow. It should be noted that modeling this boundary condition in a purely Lagrangian framework is not straightforward: assuming a horizontal Lagrangian motion on the upper boundary, the particles would soon approach the right wall creating very distorted elements that can slow down the analysis and introduce numerical issues in the solver. With the proposed approach a line of fixed Eulerian nodes is used to model the upper boundary on which the two velocity components can be easily imposed.

Cremonesi M., Meduri S., Perego U. (2020) Lagrangian-Eulerian enforcement of non-homogeneous boundary conditions in the Particle Finite Element Method, Computational Particles Mechanics, vol. 7, pp. 41-56 , DOI:10.1007/s40571-019-00245-0

A Lagrangian nodal integration method for free-surface fluid flows

A Lagrangian nodal integration method for the simulation of Newtonian and non-Newtonian free-surface fluid flows is here considered. The proposed nodal Lagrangian method uses a finite element mesh to discretize the computational domain and to define the (linear) shape functions for the unknown nodal variables, as in the standard Particle Finite Element Method (PFEM). In this approach, however, the integrals are performed over nodal patches and not over elements, and strains/stresses are defined at nodes and not at Gauss points. This allows to limit the drawbacks associated with the remeshing and leads to a more accurate stress computation than in the classical elemental PFEM.

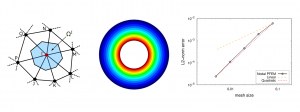
Figure: Example of nodal integration. Nodal area, contour plot of the results and graph of the error.

Franci A., Cremonesi M., Perego U., Oñate E. (2020) A Lagrangian Nodal Integration Method for Free-Surface Fluid Flows,  Computer Methods in Applied Mechanics and Engineering, vol 361, 112816, DOI:10.1016/j.cma.2019.112816

A very efficient mesh smoothing to improve the qualidy of the 3D mesh

The Lagrangian description of the PFEM requires an efficient and robust runtime mesh generator algorithm, such as the Delaunay tessellation, to create new meshes during the analysis, whenever the current ones get too distorted because of the motion of the mesh nodes. When 3D problems are considered, a computationally effective mesh-improving algorithm is
also required because, in 3D, the Delaunay tessellation loses some of its optimality properties holding in 2D so that badly shaped tetrahedra are frequently included in the triangulation, leading to unacceptably small stable time step sizes for the explicit solver. To this purpose, a novel and efficient mesh smoothing technique is here proposed, exploiting an elastic analogy that allows for the use of the same explicit and parallelizable architecture of the fluid solver. This smoothing algorithm has been specifically designed to ensure reasonably large critical time step sizes at an acceptable computational cost.

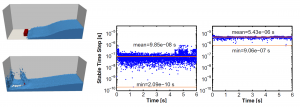
Figure: Dam break with an obstacle. The first graph represents the stable time step with ths standard Delaunay tessellation, the second one is the stable time step after the application of the proposed mesh smoothing technique. The higher quality of the 3D mesh ensures a larger stable time step size.

Meduri S., Cremonesi M., Perego U. (2019) An efficient runtime mesh smoothing technique for 3D explicit Lagrangian free surface fluid flow simulations, International Journal for Numerical Methods in Engineering, vol. 117(4), pp. 430-452, DOI:10.1002/nme.5962

Simulation of granular materials

Dense granular flows are involved in several fields of engineering and technology such as geophysics, geotechnical en-gineering, mining, pharmaceutical and alimentary industry. Their understanding and modeling are therefore of paramount importance.

From the computational point of view, dense granular flows have been approached with both discrete and continuum methods. The Discrete Element Method (DEM) is the most representative technique of the first family. A continuum approaches describe the granular material as a unique body, regardless of the number of grains contained therein. However, in a continuum framework, the computational challenge becomes the definition of a constitutive. A possible constitutive law is the so-called μ(I)-rheology.

The μ(I)-rheology relates the shear stress to the pressure via a friction coefficient depending on the so-called inertial number, a non-dimensional variable containing information of both microscopic and macroscopic scales.

Figure: Granular column collapse. Numerical and experimental results.

This work aims to shed light on the ill-conditioning problems of the constitutive model and to propose two regularized forms of the μ(I)-rheology capable to reduce the ill-conditioning of the FEM solution. The regularized methods limit the value of the apparent viscosity when the shear strain rate tends to zero, approximating accurately the response of the standard μ(I)-rheology and circumventing its endemic algebraic drawbacks. The proposed regularized models allow for the solution of large 3D problems using iterative linear solvers and maintaining limited the number of iterations.

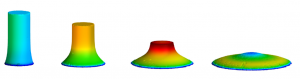
Figure: Example of collapse of a cylindrical granular column.

A fully explicit approach for the solution of the fluid dynamics problem

An explicit finite element approach to the solution of the Lagrangian formulation of the Navier-Stokes equations for weakly compressible fluids or fluid-like materials is investigated. The introduction of a small amount of compressibility is shown to allow for the formulation of a fast and robust explicit solver based on a particle finite element method. Newtonian and Non-Newtonian Bingham laws are considered. A barotropic equation of state completes the model relating pressure and density fields.

Figure: water drop fall. Example of application of the explicit solver.

Cremonesi M., Meduri S., Perego U., Frangi A. (2017) An explicit Lagrangian finite element method for free-surface weakly compressible flows, Computational Particles Mechanics, vol. 4(3), pp.357-369, DOI:10.1007/s40571-016-0122-7